0 Introduction
Convolutional neural networks(CNN) have enjoyed great success in computer vision research fields in the past few years. A number of attempts are made based on the original CNN architecture to improve its accuracy and performance. In 2014, Karen Simonyan et al. did an investigation on the effect of depth on CNNs' accuracy in large-scale image recognition (thus also proposing a series of very deep CNNs which are usually called VGG nets). The result confirmed the importance of CNN depth in visual representations.
1 Background: VGG net's ancestors
Before introducing VGG net, let's take a glance at prior convolutional neural networks.
1.1 LeNet: The Origin
Basic neural network structures(for example, multi-layer perceptron) learn patterns on 1D vectors, which cannot cope with 2D features in images well. In 1986, Lecun et al. proposed a convolution network model called LeNet-5. Its structure is fairly simple: two convolution layers, two subsampling layers and a few fully connected layers. This network was used to solve a number recognition problem. (If you need to learn more about the convolution operation, please refer to Google or Digital Image Processing by Rafael C. Gonzalez)
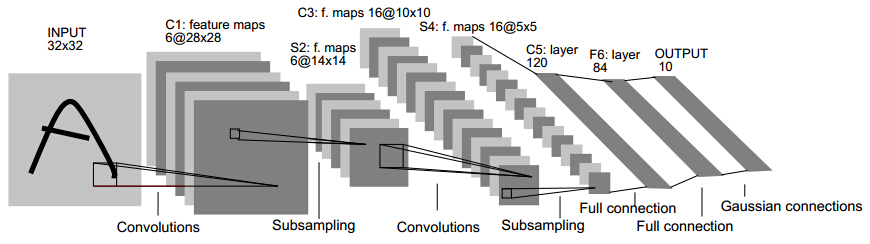
Fig. 1 Architecture of LeNet
1.2 AlexNet: The Powerful Convolution
In 2012, Alex Krizhevsky et al. won the first place in ILSVRC-2012(ImageNet Large-Scale Visual Recognition Challenge 2012) and achieved the highest top-5 error rate of 15.3% with a convolutional network model, while the second-best entry only achieved 26.2%. The network, namely AlexNet, was trained on two GTX580 3GB GPUs in parallel. Since a single GTX580 GPU has only 3GB memory, the maximum size of networks is limited. This model proved the effectiveness of CNNs under complicated circumstances and the power of GPUs. So what if the network can go deeper? Will the top-5 error rate get even lower?
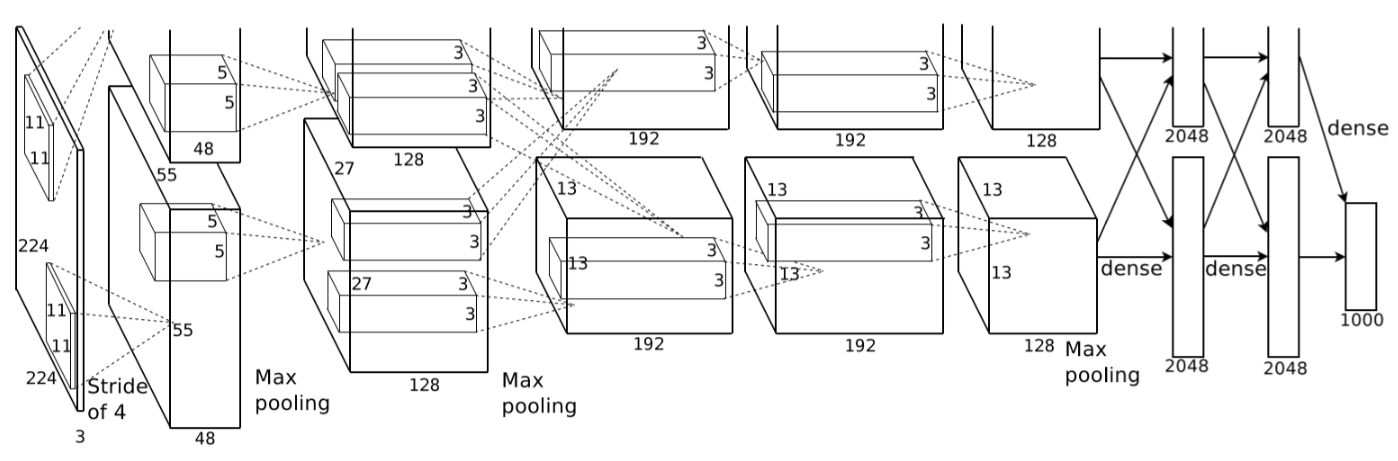
Fig. 2 Architecture of AlexNet
2 Main Contributions of VGG Nets
Here comes our hero - VGG nets. By the way, VGG is not the name of the network, but the name of the authors' group - Visual Geometry Group, from Department of Engineering Science, University of Oxford. The networks they proposed were therefore named after the group. The main contributions of VGG nets are: 1. more but smaller convolution filters; 2. great depth of networks.
2.1 Stacks of Smaller Convolution Filters
Rather than using relatively large receptive fields in the first convolution layers, Simonyan et al. selected very small 3x3 receptive fields throughout the whole net, which are convolved with the input at every pixel with a stride of 1. As is shown in the figures below, a stack of two 3x3 convolution layers has an effective receptive field of 5x5. We can also conclude that a stack of three 3x3 convolution filters has an effective receptive field of 7x7.
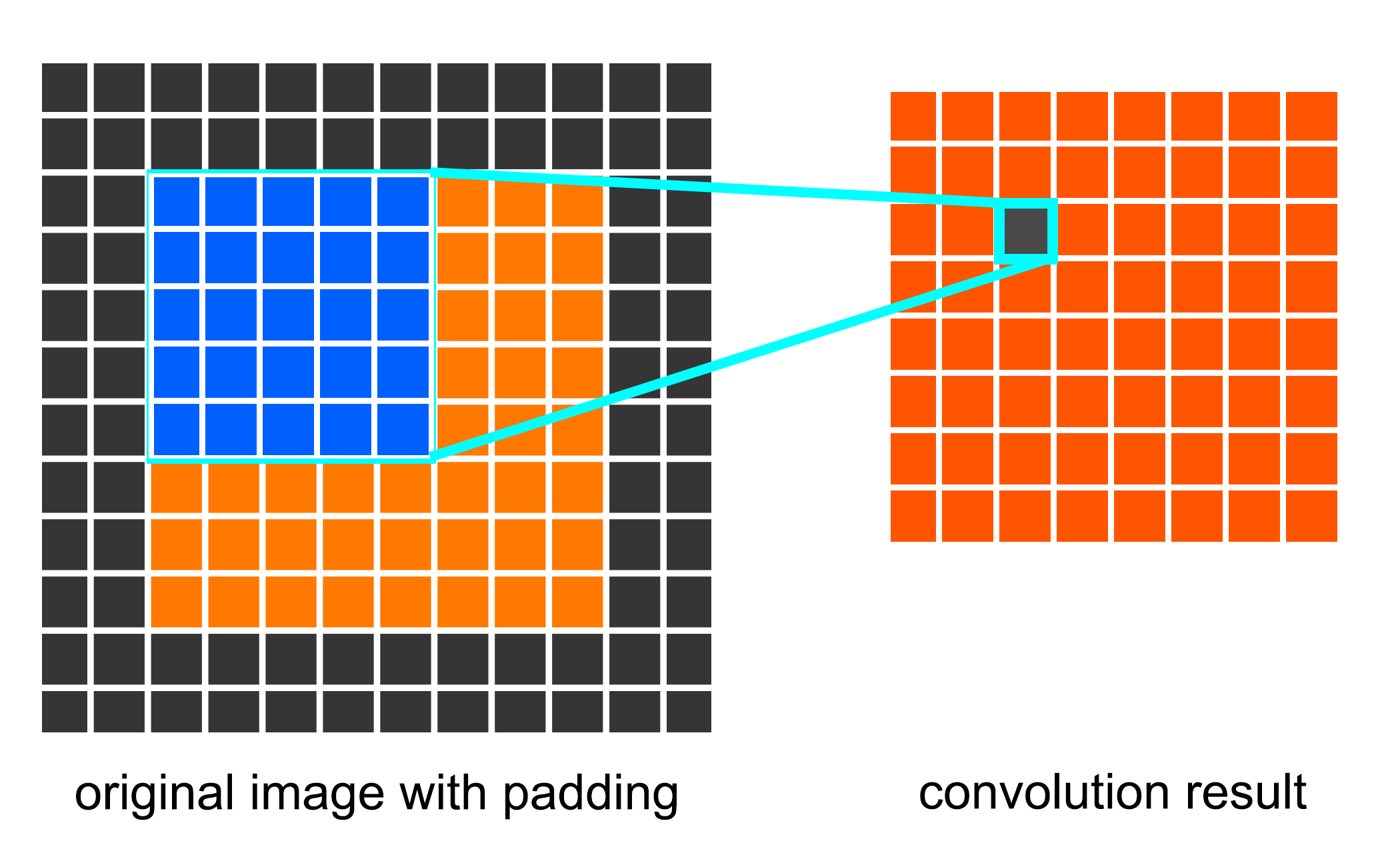
Fig. 3 A convolution layer with one 5x5 conv. filter has a receptive field of 5x5
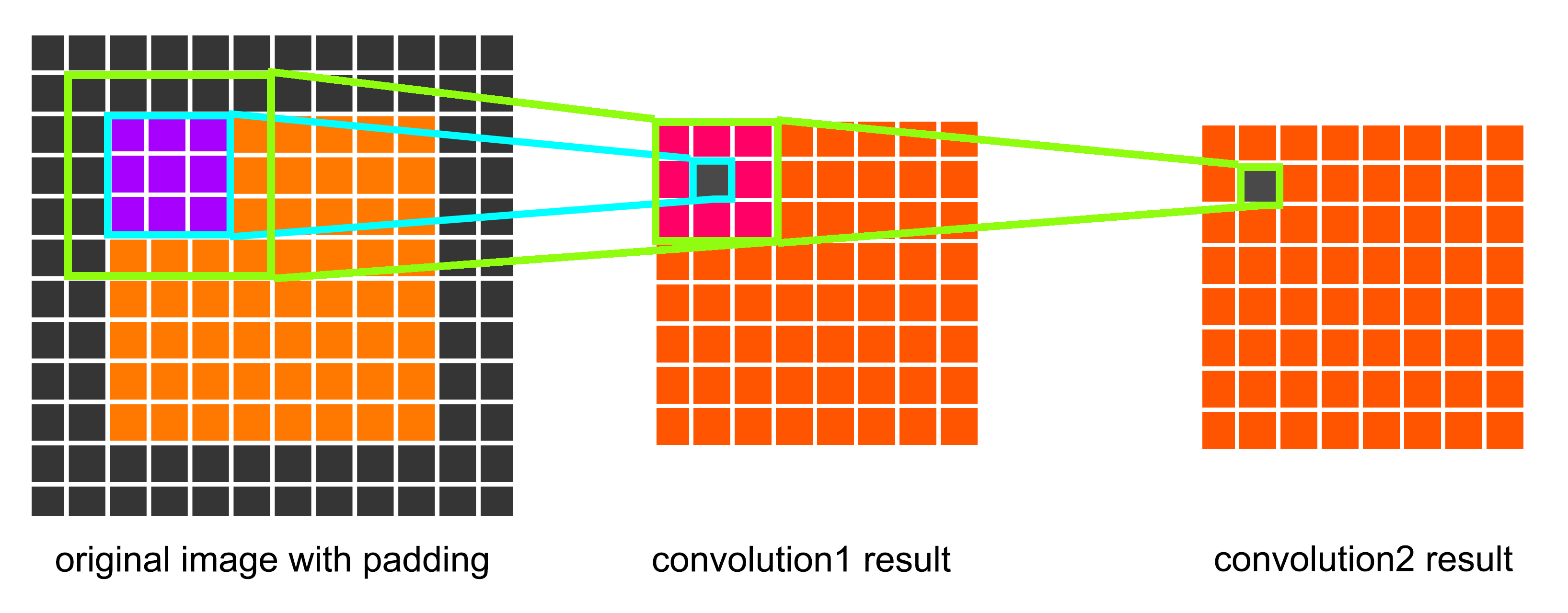
Fig. 4 A convolution layer stack with two 3x3 conv. filter also has a effective receptive field of 5x5
Now that we're clear that stacks of small-kernel convolution layers have equal sized receptive fields, why are they the better choice? Well, the first advantage is incorporating more rectification layers instead of a single one, since every convolution layer includes an activation function(usually ReLU). More rectification brings more non-linearity, and more non-linearity makes the decision function more discriminative and fit better. Also, when the receptive field isn't too large, a stack of 3x3 convolution filters have fewer parameters to train. Assuming the number of input and output channels of a convolution layer stack are equal(let's call it C) and the receptive field is 5x5, we have \(2*3*3*C*C=18C^2\) instead of \(5*5*C*C=25C^2\) parameters here. Similarly, when the receptive field is 7x7, we have \(3*3*3*C*C=27C^2\) instead of \(7*7*C*C=49C^2\). When the field gets even larger? A function with \(O(n)\) complexity only has greater advantage against an \(O(n^2)\) when \(n\) grows.
2.2 Deep Dark Fantasy
Cliches time. Just like any blogger mentioning VGG nets would do, here are the network structures proposed by Simonyan et al.
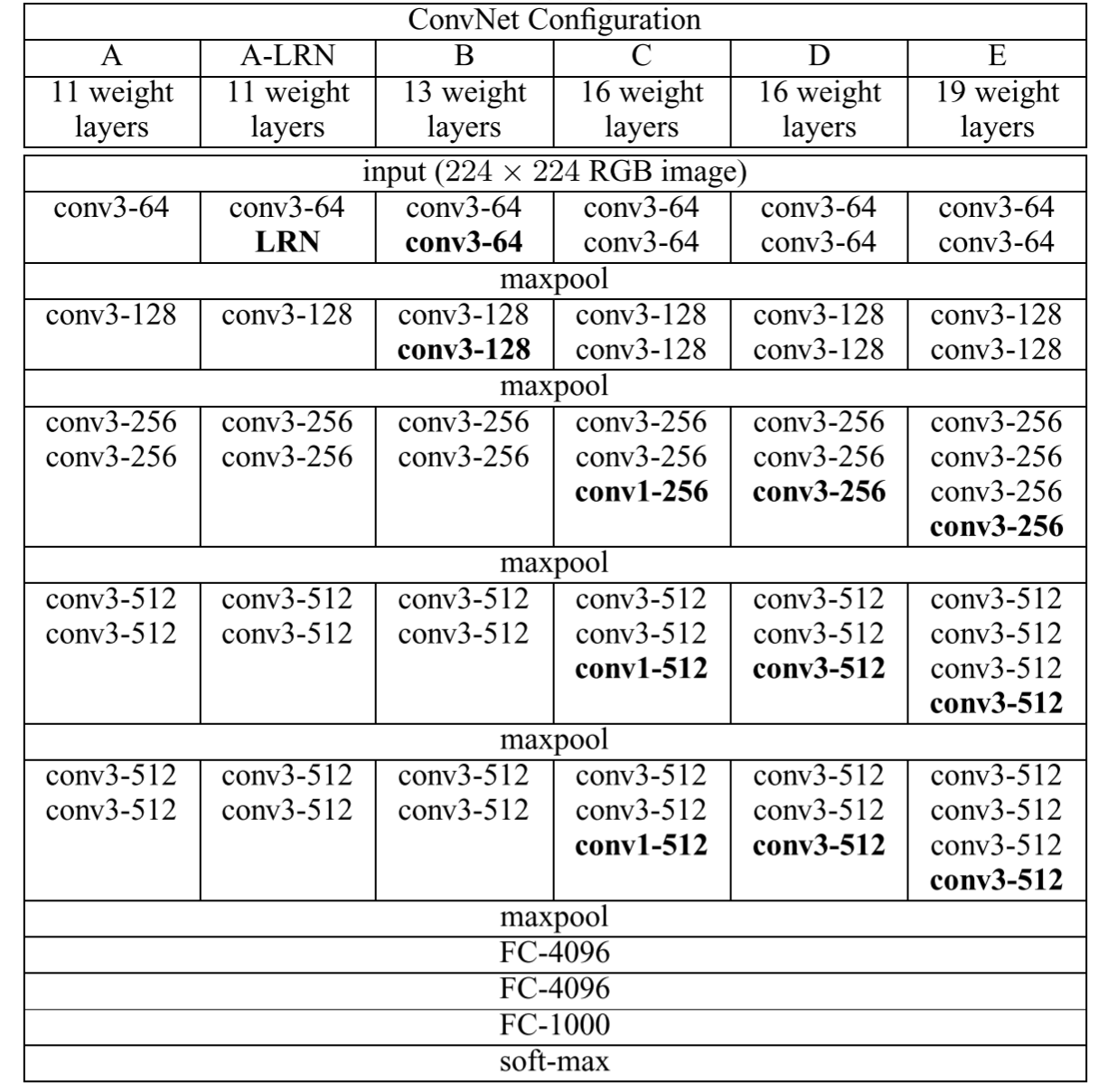
Table. 1 VGG nets of various depths
Look at the table column-by-column. Each column(A, A-LRN, B, C, D, E) corresponds to one network structure. As you can see, their networks grew from 11 layers(in net A) to 19 layers(in net E). Each time something is added to the previous net, it would appear bold. Clearly, LRN(Local Response Normalization) didn't work well in this case(actually, A-LRN net performed worse than A, while consuming much more memory and computation time), and was thus removed.
What's worth mentioning are the 1x1 convolution layers appearing in network C. This is a way to increase non-linearity(also by introducing activation functions) of the decision function while also keeping the size of the receptive fields unchanged.
3 Training & Evaluation
Bad initialization could stall learning due to the instability of gradient deep networks. Therefore, the authors first trained the network A, which is shallow enough to be trained with random initialization. Then, the next networks (B to E) are initialized with the pre-trained models, and only weights of the new layers are randomly initialized.
In spite of the larger number of parameters and the greater depth of our nets compared to AlexNet, the nets required less epochs to converge due to the implicit regularization imposed by greater depth, smaller convolution filter sizes and the pre-initialization of certain layers. They also generalize well to other datasets, achieving state-of-the-art performances. Results of VGG nets in comparison against other models in ILSVRC are shown in the table below.
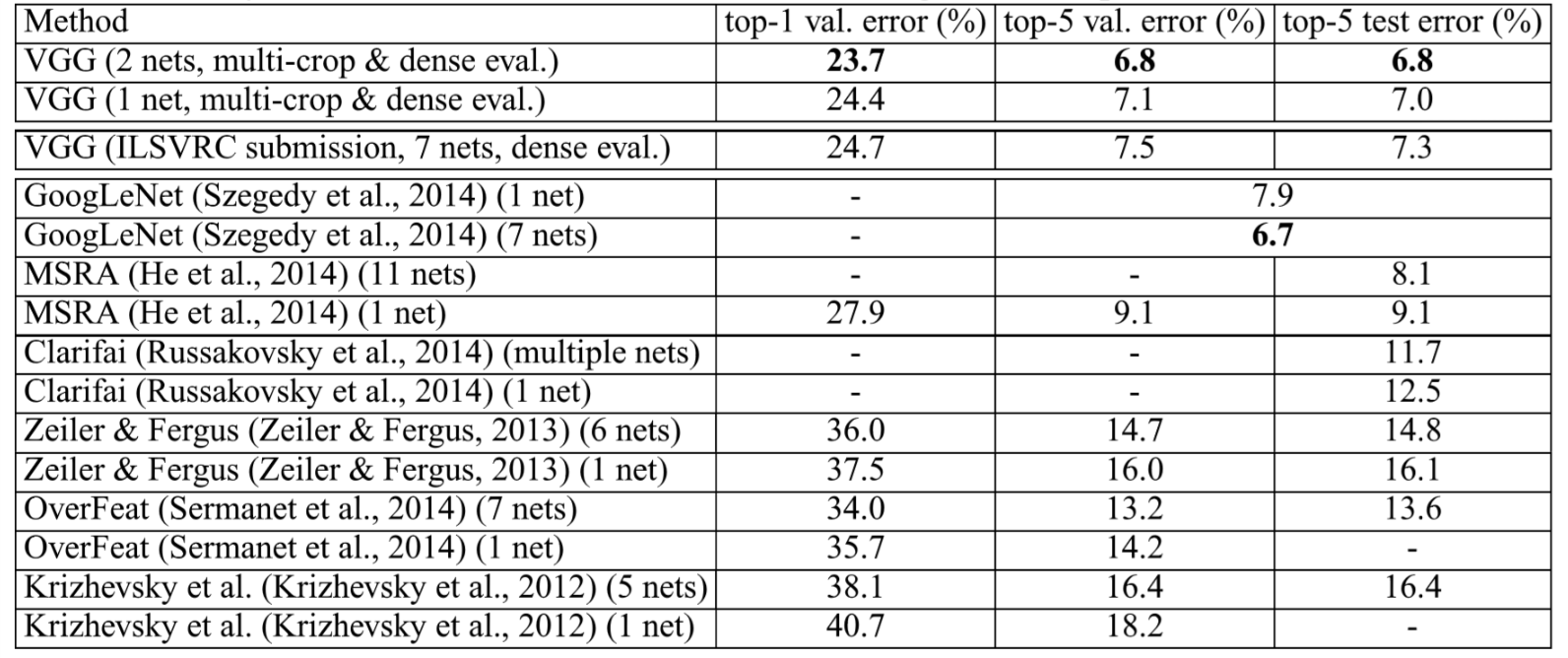
Table. 2 VGG net performance, in comparison with the state of the art in ILSVRC classification
In conclusion, the representation depth is beneficial for the classification accuracy, and that state-of-the-art performance on the ImageNet challenge dataset can be achieved using a conventional ConvNet architecture (LeCun et al., 1989; Krizhevsky et al., 2012) with substantially increased depth.
You might ask: Why not even deeper, with more powerful GPUs(the authors used Titan Black), we can absolutely train deeper networks that perform better! Not exactly. Problems arose as the networks get too deep, and this is where ResNet comes in.